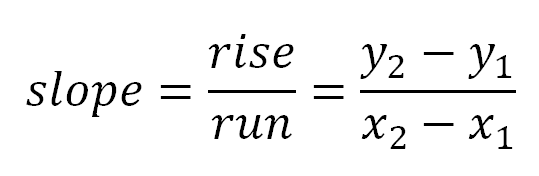Monthly Archives: August 2015

Aug 23 2015

Tips for Finding the Slope of a Straight Line

Graphing

HOW TO FIND THE SLOPE OF A STRAIGHT LINE

Slope is a measure that indicates how steep or shallow a straight line is:

  • A line with greater slope is steeper.
  • A line with less slope is shallower.
  • A horizontal line has zero slope.

Slope Sign

Slope can be positive or negative:

  • A line with positive slope slants upward.
  • A line with negative slope slants downward.
  • A line with zero slope is horizontal.

Slope Sign B

The slope of a straight line equals rise over run.

  • The rise between two points is vertical. It’s the change in y.
  • The run between two points is horizontal. It’s the change in x.

Slope Eqn

TIPS FOR FINDING SLOPE

From the graph of a straight line, determine the slope as follows:

  • Mark two points on the line.
  • Read the x- and y-coordinates of the two points, (x1, y1) and (x2, y2).
  • Subtract y2 – y1 to get the rise.
  • Subtract x2 – x1 to get the run.
  • Divide the rise by the run.

Slope Triangle

Here are a few tips:

  • When choosing the two points, try to find points where both x and y are easy to read without interpolating. This isn’t always possible: In that case, at least one coordinate should be easy to read without interpolating.
  • Choose two points far apart. This reduces the relative error in interpolating.
  • Make sure that both points lie on the straight line. Don’t choose a point that’s close to the line, but doesn’t lie on it.

EXAMPLE OF HOW TO DETERMINE SLOPE

Example: Find the slope of the straight line in the graph below.

Slope Example

Solution: First, choose two points on the line. Ideally, these points should be far apart and easy to read.

In this case, it’s easy to read both the x- and y-coordinates for the leftmost and rightmost points shown in the graph. So let’s choose those.

Slope Example 2

  • The leftmost point has coordinates (0, 3).
  • The rightmost point has coordinates (10, 8).

Subtract the y-values to determine the rise:

y2 – y1 = 8 – 3 = 5

Subtract the x-values to determine the run:

x2 – x1 = 10 – 0 = 10

(In coordinate graphing, recall that x is horizontal and y is vertical.)

Divide the rise by the run to find the slope:

Slope Example 3

The slope of the line is 0.5.

Check: You can check your answer as follows.

Look at the graph. Starting from (0, 3), the next point that’s easy to read is (2, 1).

From (0, 3) to (2, 1), the line goes one unit up (vertically) and 2 units over (horizontally).

The ratio of the rise to the run is 1 to 2. Divide the rise (of 1) by the run (of 2). The slope is 0.5. ♦

CHRIS MCMULLEN, PH.D.

Copyright © 2015 Chris McMullen, author of the Improve Your Math Fluency series of math workbooks

Newest release:

  • Basic Linear Graphing Skills Practice Workbook

Related books:

  • Trigonometry Essentials Practice Workbook with Answers
  • Learn or Review Trigonometry Essential Skills
  • Algebra Essentials Practice Workbook with Answers
  • Systems of Equations: Simultaneous, Substitution, Cramer’s Rule
Aug 12 2015

Memory Tip for Sine, Cosine, and Tangent of Special Angles (Trigonometry)

Trig Table

TRIGONOMETRY MEMORY TIP

There is a simple way to remember the sine, cosine, and tangent of special trigonometry angles.

The special trig angles are 0º, 30º, 45º, 60º, and 90º. What makes these angles special? The 30º-60º-90º triangle is one-half of an equilateral triangle, while the 45º-45º-90º triangle is one-half of a square. In both cases, the trig functions (sine, cosine, and tangent) can be expressed as simple ratios.

Here is the trick for quickly working out the sine, cosine, and tangent of 0º, 30º, 45º, 60º, and 90º.

STEP 1: Special angles.

Write the special angles in order.

Trig Table top

STEP 2: Integers.

Write the integers 0 thru 4 in order.

Trig Table numbers

STEP 3: Squareroots.

Squareroot each number.

Trig Table roots

STEP 4: Find the sine of theta.

Divide each number by 2.

Trig Table sine

These are the sine of 0º, 30º, 45º, 60º, and 90º.

It’s that simple. Here’s a recap:

  • Write the numbers 0 thru 4.
  • Squareroot each number.
  • Divide each number by 2.

STEP 5: Find the cosine of theta.

Just write the previous numbers in reverse order.

Trig Table cos

Why does this work? Because the sine of theta equals the cosine of the complement of theta: sin(θ)=cos(90º–θ). What’s opposite to theta is adjacent to its complement.

STEP 6: Find the tangent of theta.

Divide sine theta by cosine theta.

Trig Table tan

TRIG CHART

This chart shows all of the steps together.

Trig Table Tips

  • Write the special angles.
  • Write the integers 0 thru 4.
  • Squareroot each number.
  • Divide each number by 2. This gives you sine of theta.
  • Write the numbers in reverse order. This gives you cosine of theta.
  • Divide the previous two rows (sine over cosine). This gives you tangent theta.

NOTE

There are two different, yet equivalent ways, to write the above chart.

That’s because of the following properties of irrational numbers:

Roots

So, for example, there are alternative ways to express the following trig values:

Trig Values

The chart on this blog uses standard form. Most math courses use standard form, which means that there no irrational numbers (like root 2) in the denominator.

Sometimes you find the trig table in another nonstandard form. In that form, you see 1 over root 2 in place of root 2 over 2, and you see 1 over root 3 in place of root 3 over 3.

It’s important to realize that both forms are correct. The standard form, however, is expected in most math courses.

CHRIS MCMULLEN, PH.D.

Copyright © 2015 Chris McMullen, author of the Improve Your Math Fluency series of math workbooks

  • Trigonometry Essentials Practice Workbook with Answers
  • Learn or Review Trigonometry Essential Skills
  • Trigonometry Flash Cards (for Kindle)
  • Algebra Essentials Practice Workbook with Answers
  • Systems of Equations: Simultaneous, Substitution, Cramer’s Rule
  • Other volumes cover fractions, long division, arithmetic, and more
  • Also look for books on the fourth dimension, astronomy, conceptual chemistry, and more