FIBONACCI SEQUENCE
The Fibonacci sequence adds consecutive terms:
- 1
- 1
- 1 + 1 = 2
- 2 + 1 = 3
- 3 + 2 = 5
- 5 + 3 = 8
- 8 + 5 = 13
- 13 + 8 = 21
- 21 + 13 = 34
- 34 + 21 = 55
- 55 + 34 = 89
Since the last two terms were 55 and 89, we would add these together to get 89 + 55 = 144.
Then you would add 144 and 89 to make 233, and so on.
I saw a cool pattern involving the Fibonacci sequence recently at the Mathemagical Site:
Fibonacci Triples via Mathemagical Site
This involves Fibonacci triples.
A Fibonacci triple consists of three consecutive numbers from the Fibonacci sequence, such as:
- 1, 1, 2
- 1, 2, 3
- 2, 3, 5
- 3, 5, 8
- 5, 8, 13
- 8, 13, 21
- 13, 21, 34
As shown on the Mathemagical Site, the square of the middle number is always one less or one more than the product of the first and third numbers:
Here are a few examples:
- (2, 3, 5): 3 x 3 = 2 x 5 – 1
- (3, 5, 8): 5 x 5 = 3 x 8 + 1
- (5, 8, 13): 8 x 8 = 5 x 13 – 1
Curious about this, I’ve been working through the algebra, and finally came up with an algebraic proof, which follows.
My proof is algebraic and not necessarily obvious, but since I worked it out, I thought I would share it here. 🙂
We begin with two facts about the Fibonacci sequence:
These are two different ways of saying that if you add two consecutive numbers from the Fibonacci sequence, you get the next number in the sequence.
Now solve for xn in each sequence:
Multiply these together:
Foil this out:
Recall that
Plug this into the first term on the right-hand side of the previous equation:
Distribute:
Two of these terms cancel (the remaining terms are rearranged):
Believe it or not, this basically concludes the proof. The remainder is basically interpreting this result.
This is a recursion relation that relates the square of the n-th term to the square of the previous term (xn-1 times itself).
Following is the Fibonacci sequence, labeling values of n:
- n = 1 is 1.
- n = 2 is 1.
- n = 3 is 2.
- n = 4 is 3.
- n = 5 is 5.
- n = 6 is 8.
- n = 7 is 13.
- n = 8 is 21.
Let’s plug in n = 3 and see what happens:
If instead you plug in n = 4, you get:
Now just plug in these two expressions (x3x3 – x4x2 and x4x4 – x5x3) into the previous recursion relation and you can prove that all of the Fibonacci triples satisfy one of the following relations:
That is, if x3x3 – x4x2 = 1 and x4x4 – x5x3 = -1, the previous recursion relation gives similar expressions for x5x5 – x6x4, x6x6 – x7x5, and so on.
CHRIS MCMULLEN, PH.D.
Copyright © 2015 Chris McMullen, author of the Improve Your Math Fluency series of math workbooks
- Algebra Essentials Practice Workbook with Answers
- Trigonometry Essentials Practice Workbook with Answers
- Learn or Review Trigonometry: Essential Skills



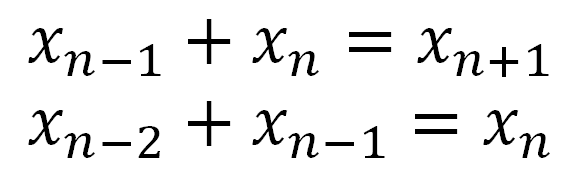
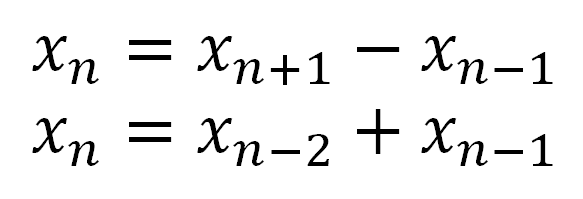


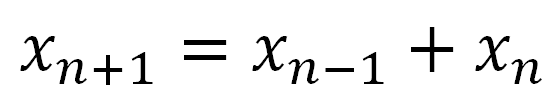




Reblogged this on Mathemagical Site and commented:
This is a simple algebraic proof of a certain pattern of Fibonacci triples that I have posted a few days ago.
Note; Comments are turned off here. Please visit the original post.
Thank you for sharing my proof. I appreciate it much. 🙂
You are welcome.